x2-11x+28=0: Mathematical Solution

x2-11x+28=0

In mathematics, x2-11x+28=0 quadratic equations inhabit an essential and intriguing position. They are apparent in numerous domains, from physics and engineering to ordinary problem-solving scenarios. Between these quadratic equations, x2-11x+28=0 is a noteworthy one. This article aims to investigate the particulars of this equation deeply, clarifying its roots, factors, and the methodologies working for its resolution. So, if you’ve ever found yourself perplexed when meeting the equation x2-11x+28=0, fear not! Please last reading to elucidate its paradox.

Welcome to traveling quadratic equations, an integral share of algebra and mathematics. This article will investigate quadratic equations, concentrating on the equation x2-11x+28=0. Throughout this comprehensive conversation, we will expose the general concept of quadratic equations, travel a range of approaches to solve them, and behave in a deep dive into an exact case study to comprehend the practical requests of these equations.

What Establishes a Quadratic Equation x2-11x+28=0?

Before we decode the particulars of our equation, let’s take an instant to reenter the core idea of quadratic equations. A quadratic equation is a second-degree polynomial, typically represented in ax^2 + bx + c = 0. Here, ‘a,’ ‘b,’ and ‘c’ are coefficients, while ‘x’ is the mutable we aim to resolve for.

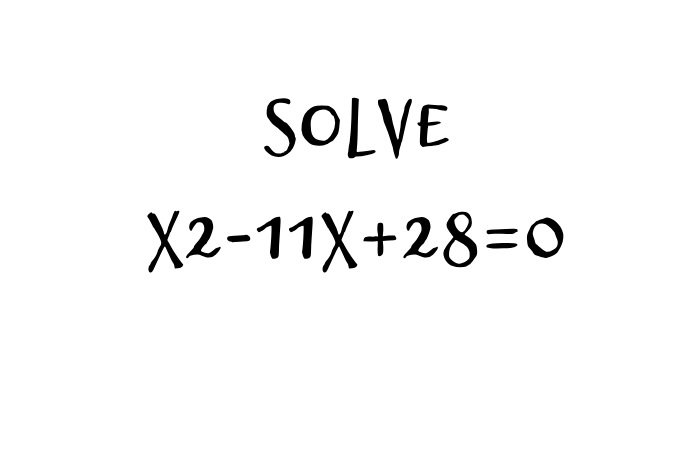
Understanding Quadratic Equations x2-11x+28=0

Before we dump into the particulars of equation x^2 – 11x + 28 = 0, let’s first find a foundational understanding of quadratic equations.

Quadratic Equation Definition

We must grasp the essence of quadratic equations to embark on this trip. First, a quadratic equation is a second-degree polynomial characterized by the squared mutable. The most important form of a quadratic equation is expressed as:

Equation : ax^2 + bx + c = 0

‘a,’ ‘b,’ and ‘c’ equations are designated constants, while ‘x’ signifies the variable. The equation x2-11x+28=0 precisely brings into line with this standard form.

General Form of a Quadratic Equation

Understanding the overall form of a quadratic equation is vital as it underpins the foundation of these equations. Meaningful this structure, we can categorize the coefficients ‘a,’ ‘b,’ and ‘c.’ For our careful equation, ‘a’ is 1, ‘b’ is -11, and ‘c’ is 28.

x^2 – 11x + 28 = 0  – Equation

Agreements stress the equation: x^2 – 11x + 28 = 0.

Factoring of the Quadratic Equation

One method to resolve quadratic equations is by factorization. In this case, we can issue the equation as darks:

x^2 – 11x + 28 = 0 (x – 4)(x – 7) = 0

Finding the Roots

To learn the solutions (roots) of the equation, we set apiece subject equal to zero:

x – 4 = 0 => x = 4 x – 7 = 0 => x = 7

So, the origins of the equation x^2 – 11x + 28 = 0 are x = 4 and x = 7.

Graphical Representation

Let’s imagine the answers by graphing the equation.

Real-Life Applications

Quadratic equations are not just theoretical ideas; they have practical requests in various arenas.

Physics

In physics, quadratic equations are used to describe objects’ gestures under the effect of gravity. The equation is x^2 – 11x + 28 = 0. Strength signifies the time it takes to spread a certain height when thrown up.

Solving Quadratic Equation x2-11x+28=0

Quadratic equations are mathematical problems that can be tackled using various methods. Let’s explore two prominent techniques:

Factoring

Factoring is a technique to solve quadratic reckonings that can be easily broken down. However, for equations as complex as x2-11x+28=0, factoring may not be the most straightforward approach.

Quadratic Formula

The quadratic formula is a versatile and universally applicable approach to solving quadratic equations. This formula, often called upon, is:

x = (-b ± √(b^2 – 4ac)) / 2a – Equation

With this formula, we become the roots of the equation on behalf of the standards of ‘x’ that decrease the equation equal to zero.

A Case Study: x^2-11x+28=0

Interestingly, we now go our upkeep to the exact equation x2-11x+28=0. Our examination will include a step-by-step review using the quadratic formula.

Step 1: Recognizing the Coefficients

To initiate this trip, we must first identify the constants. ‘a’ is 1, ‘b’ is -11, and ‘c’ equation is 28.

Step 2: Smearing the Quadratic Formula

We can now apply the quadratic formula with the coefficients in our grasp. The equation takes shape as follows:

• x = (-(-11) ± √((-11)^2 – 4 * 1 * 28)) / (2 * 1)

In the pursuit of a solution, we simplify the equation, leading to:

• x = (11 ± √(121 – 112)) / 2
• x = (11 ± √9) / 2

Step 3: Finding the Roots

As the equation begins to form, we expose two potential solutions:

• x = (11 + 3) / 2 = 7
• x = (11 – 3) / 2 = 4

Therefore, the origins of the equation x2-11x+28=0 are exposed as x = 7 and x = 4.

Factoring the Quadratic Equation of x2-11x+28=0

Let’s immerse ourselves in the intricate procedure of factoring the equation x2-11x+28=0.

Identify the Coefficients

• A = 1
• B = -11
• C = 28

To begin the factoring process, it is authoritative to categorize the coefficients of the equation, which in our condition are A = 1, B = -11, and C = 28.

Find Two Numbers

Factoring a quadratic equation necessitates discovering two numbers that, when multiplied, yield the product ‘A * C’ (in this instance, 1 * 28) and simultaneously add up to ‘B’ (which, in our case, is -11). The numbers we seek are -7 and -4, for the product of (-7) * (-4) indeed equals 28, and their sum, (-7) + (-4), equivalently amounts to -11.

Must Read:

• 2×2-3x- 5 = 0: Solving The Complex Equation
• x2 + (y – 3√2x)2 = 1: Solving The Equation

Rewrite the Equation

With our numbers identified, we can now proceed to rewrite the equation:

x² – 7x – 4x + 28 = 0

Grouping and Factoring

An essential step in the factoring process involves grouping the terms appropriately, which sets the stage for factoring by grouping. The equation in its grouped form appears as follows:

x(x – 7) – 4(x – 7) = 0

Apply the Distributive Property

Our next step involves the application of the distributive property, facilitating the factorization of the equation by extracting the common term (x – 7):

(x – 7)(x – 4) = 0

Finding the Roots

With the equation successfully factored in, we can now uncover its roots. This is achieved by setting each factor equal to zero:

1. x – 7 = 0
2. x – 4 = 0

Solving for ‘x’

Now that we’ve isolated the two factors, we proceed to solve for ‘x’ in each of the equations:

1. x = 7
2. x = 4.

The Roots of the Quadratic Equation of x2-11x+28=0

Now that we’ve solved both equations derived from the factored form, we have two possible values for x:

x = 7

x = 4

These values represent the roots or solutions to the quadratic equation x2 – 11x + 28 = 0. In other words, if we substitute these values back into the original equation, it will hold:

For x = 7:

7² – 11(7) + 28 = 49 – 77 + 28 = 0

For x = 4:

4² – 11(4) + 28 = 16 – 44 + 28 = 0

Both values of x satisfy the equation, making them the roots of the quadratic equation.

Significance of the Solutions of x2-11x+28=0

The solutions, x=7 and x=4, carry deep significance in the setting of the original problematic. In real-world requests, quadratic equations often perfect motion, geometry, and optimization situations. For example, if the quadratic equation signifies the height of an object thrown into the air, the solutions correspond to the time points when the thing spreads certain heights. Understanding and interpreting these solutions are energetic in physics, engineering, and economics.

Graphical Representation

Imagining the quadratic equation x2 – 11x + 28 = 0 adds another understanding coating. When plotted on a Cartesian plane, the equation forms a parabola. The roots, x=7 and x=4, correspond to the points where the parabola symbols are on the x-axis. This graphical picture reinforces the algebraic solutions and delivers an intuitive grasp of the equation’s behavior.

Relationship with Factoring

Factoring is another method to resolve quadratic equations, and it can deliver insights into the scenery of the solutions. In the case of x2 – 11x + 28 = 0, factoring involves finding two binomials whose formation equals the original look. The factored form is (x−7)(x−4)=0, skimpy that x=7 and x=4 are indeed the roots. This connection between factoring and the quadratic formula showcases the elegance and adaptability of mathematical techniques.

Applications in Real-world Scenarios

Quadratic equations manifest in various applied situations, counting x2 – 11x + 28 = 0. Consider a business owner examining profit and loss or an environmentalist studying populace growth. These scenarios can be demonstrated using quadratic equations, with the solutions offering valuable visions into critical points and tendencies. Solving such equations is a powerful tool in executive and problem-solving across diverse arenas.

Conclusion

The quadratic equation x^2 – 11x + 28 = 0 is an essential mathematical idea with real-world applications. By factoring and solving it, we found that it has two roots: x = 4 and x = 7. Sympathetic quadratic equations are vital in mathematics and numerous fields, making it a valued skill for problem-solving. To sum up, delving into quadratic equations has been a fascinating trip.

In this article, we have threadbare the fundamental ideas of nearby quadratic equations and the methodology of solving them using the quadratic formula. We have witnessed the practical insinuations through a specific case study, namely x2-11x+28=0. Also, we have explored the visual picture of quadratic equations via parabolic graphs and highlighted their real-world significance in numerous requests.

Also Read: Big Data Indoglobenews.co.id

Related Searches to x2-11x+28=0

x2-11x+28=0
x2 11x 28-0
28 0
x ^ 2 – 11/4 * x + 15/8 = 0
x ^ 2 + 1/(x ^ 2) – 11
6x ^ 2 + 11x – 10
x2 11x 28 0 quadratic formula
x2 11x 28 0 answer